Se você está procurando uma ferramenta online para calcular a média, desvio padrão e variância, compartilhamos com você esta Calculadora de Desvio Padrão. Nossa ferramenta matemática, além de calcular o desvio padrão, também lhe dá o passo a passo de toda a operação, oferecendo diferentes resultados valiosos como a variância e a média.
Esta calculadora, além de ajudá-lo a fazer o cálculo de forma rápida e fácil, oferece a oportunidade de aprender passo a passo a operação de desvio padrão. Abaixo também compartilharemos conceitos básicos sobre o tema que podem lhe interessar caso tenha alguma dúvida, para que possa resolvê-la imediatamente.
O que é Desvio Padrão?
O desvio padrão é uma medida da dispersão dos dados e é um dos métodos básicos de análise estatística. É comumente abreviado como DP e é representado pela letra grega 'σ', indicando o quanto os valores se desviaram do valor médio. Um desvio padrão baixo significa que os valores tendem a ficar próximos da média, enquanto um desvio padrão alto nos diz que os valores estão longe da média.
Fórmula do Desvio Padrão
A fórmula do desvio padrão é calculada usando a raiz quadrada da variância. A variância de um conjunto de dados é a média das distâncias quadradas entre o valor médio e cada valor de dados.

Na fórmula, μ é a média, x é cada valor dos dados e N é o número total de dados. Se seus dados corresponderem a uma amostra, você deve usar a seguinte fórmula:
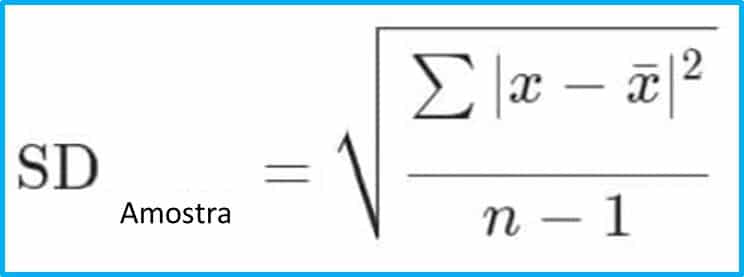
Como Calcular o Desvio Padrão
Para calcular o desvio padrão, apresentamos 6 passos muito simples a seguir, usando um conjunto de 6 dados como exemplo:

- Encontre a média: Some todos os dados e divida pelo número de dados.
- Calcule o desvio da média: Subtraia a média de cada um dos dados.
- Eleve ao quadrado cada desvio: Multiplique cada valor por si mesmo para obter um resultado positivo.
- Some todos os desvios quadrados.
- Calcule a variância: Divida a soma dos quadrados por (n-1) para amostras ou N para a população.
- Calcule a raiz quadrada da variância: O resultado é o desvio padrão.






Finalmente, temos que o Desvio Padrão = 11,31, o que indica que cada dado se desvia, em média, 11,31 pontos da média.
Aplicação do Desvio Padrão na Vida Real
O desvio padrão é usado para medir a dispersão de valores em um conjunto de dados. Pessoas e empresas o utilizam em diferentes campos para obter uma melhor compreensão dos dados.
Previsão do Tempo
O desvio padrão é amplamente utilizado para entender a variação nas temperaturas diárias e mensais em diferentes cidades.
Cuidados Médicos
Analistas de seguros calculam o desvio padrão da idade das pessoas que seguram para entender a variação de idade entre seus clientes.
Imóveis
No setor imobiliário, é usado para descobrir o desvio padrão dos preços da habitação em áreas residenciais específicas.
Recursos Humanos
Para saber o tipo de salário que pode ser oferecido em uma empresa em uma determinada área, o especialista em recursos humanos calcula o desvio padrão dos salários.
Marketing
Os profissionais de marketing usam o desvio padrão para entender o desempenho de seus anúncios e a variação na receita gerada.
